悢撈挻擄栤偺夝偒曽(偍栮偝傫偺僫儞僾儗嘦乯
悢撈挻擄栤偺夝偒曽(偍栮偝傫偺僫儞僾儗嘦乯
XY wing
侾丏XYwing偲偼
丂悢撈偺XY僂傿儞僌乮XYwing乯偼丄悢撈僷僘儖偺夝朄僥僋僯僢僋偺堦偮偱偡丅XY僂傿儞僌偼丄摿掕偺僷僞乕儞偑尰傟偨偲偒偵揔梡偱偒傞夝朄偱偡丅婎慴曇偱偼忋媄朄侾(3儅僗寛傔丄俀/俁僄儕傾乯偲偟偰愢柧偝傟偰偄傑偡丅懳徧揑側3偮偺僄儕傾乮type1乯枖偼2偮偺僄儕傾乮type俀乯偵偁傞3儅僗偵傛傝桿摫偟偰丄懳徧揑埵抲偵偁傞儅僗傪寛掕偡傞媄朄偱偡丅
丂嘆懳徧揑3僄儕傾
丂嘇堎側傞2働僞偺3悢帤
丂嘊2夞偯偮弌尰丂丂偱桳岠偵側傝傑偡丅偱偡偐傜45-57-47偺慻傒崌傢偣偼OK偱偡偑丄45-45-47傗45-457-457偼揔梡偱偒傑偣傫丅
XY僂傿儞僌偼丄偙偺傛偆側僔儞僾儖側榑棟揑側悇榑傪梡偄偰丄悢撈偺擄偟偄晹暘傪夝偔偺偵栶棫偪傑偡丅挻擄栤傪夝愅偡傞偵偼丄XY僂僀儞僌偵Type1偲Type2偺2庬椶偑偁傞偙偲傪棟夝偟丄嬱巊偡傞昁梫偑偁傝傑偡丅
俀丏XYwing丂type1
丂type1偼忋媄朄侾偱3儅僗寛傔丄3僄儕傾偱懠偺儅僗偺悢帤傪寛掕偡傞曽朄偱偡丅XY僂僀儞僌偼X僂僀儞僌偵斾妑偟偰尒偮偗傗偡偔丄挻擄栤傪夝愅偱偼懡梡偝傟傑偡丅椺戣3偵偰僾儘僙僗傪妋擣偟傑偡丅椺戣3傪拞媺儗儀儖偺媄朄偱夝愅偟丄搑拞宱夁偵帄傝傑偟偨丅偙傟埲忋偼拞媺偺媄朄偱偼夝愅偱偒傑偣傫丅
悢婰擖偝傟偨儅僗偺偆偪丄2悢帤偺壜擻惈偺偁傞儅僗傪庢傝弌偟傑偡丅偙傟偵傛傝倃倄僂僀儞僌偑尒偮偗傗偡偔側傝傑偡丅幚嵺偺扵偟曽偼丄師偺捠傝偱偡丅
丂侾乯2悢帤儅僗偱侾乣俋棑偺偦傟偧傟偺a乣i傪傒偰丄2偮埲忋2悢帤儅僗偑偁傞偐斲偐傪妋擣偟傑偡丅
丂丂丂佀椺戣3偱偼3棑埲奜偼奩摉偟傑偡丅
丂俀乯1棑偵偼3偮偺2悢帤儅僗偑偁傝傑偡(1a,1f,1i)丅偦傟偧傟懠偺僄儕傾偱懳徾偲側傞2悢帤儅僗偑偁傞偐妋擣偟傑偡丅
丂丂 佀1棑偱偼(1a,1f)+(8a,8f)偲(1f,1i)+(4f,4i)偺俀偮偺儁傾偑妋擣偱偒傑偡丅
丂俁乯儁傾偺4偮偺儅僗偺3偮偺儅僗偑丄ab,bc,ca偺慻傒崌傢偣偵側偭偰偄傞偐妋擣偟傑偡丅
丂丂丂(1a,1f)+(8a,8f)偱偼丄69,78,57,57偱奩摉偟傑偣傫丅
丂丂佀(1f,1i)+(4f,4i)偱偼丄78(1f),17(1i),18(4i)偑1-7-8偱奩摉偟丄惂尷偡傞儅僗偱偡丅
丂係乯廬偭偰1,7,8偼1f,1i,4i偱愯傔傜傟傑偡偺偱丄4f偑惂尷偝傟傞儅僗偵側傝8偑擖傞壜擻惈偼偁傝傑偣傫丅
丂丂佀4f偼5偵側傝傑偡丅偙傟埲崀偼拞媺偺媄朄偱夝愅偟夝摎傪摼傜傟傑偡丅
丂(拲乯亂倃倄僂僀儞僌亃偺墿怓儅僗偑惂尷偡傞3偮偺儅僗偱丄奃怓儅僗偑惂尷偝傟傞儅僗偱偡丅
丂亂椺戣3亃丂丂丂丂丂丂丂丂丂丂丂丂亂搑拞宱夁亃丂丂丂丂丂丂丂丂丂丂亂悢婰擖亃丂丂丂丂丂丂丂丂丂丂丂丂亂XY僂僀儞僌亃丂丂丂丂丂丂丂丂丂亂夝摎亃

摨條偵椺戣4傪椺偵偲傞偲丄師偺傛偆偵側傝傑偡丅
丂侾乯2悢帤儅僗偱侾乣俋棑偺偦傟偧傟偺a乣i傪傒偰丄2偮埲忋2悢帤儅僗偑偁傞偐斲偐傪妋擣偟傑偡丅
丂丂丂佀椺戣4偱偼7棑埲奜偼奩摉偟傑偡丅
丂俀乯1棑偵偼3偮偺俀悢帤儅僗偑偁傝傑偡(1a,1f,1g)丅偦傟偧傟懠偺僄儕傾偱懳徾偲側傞2悢帤儅僗偑偁傞偐妋擣偟傑偡丅
丂丂 佀1棑偱偼(1a,1f)+(6a,6f)偲(1f,1g)+(6f,6g)偺俀偮偺儁傾偑妋擣偱偒傑偡丅
丂俁乯儁傾偺4偮偺儅僗偺3偮偺儅僗偑丄ab,bc,ca偺慻傒崌傢偣偵側偭偰偄傞偐妋擣偟傑偡丅
丂丂丂(1a,1f)+(6a,6f)偱偼丄67,18,13,15偱奩摉偟傑偣傫丅
丂丂佀(1f,1g)+(6f,6g)偱偼丄18(1f),58(1g),15(6f)偑1-5-8偱奩摉偟傑偡丅
丂係乯廬偭偰1,5,8偼1f,1g,6f偱愯傔傜傟傑偡偺偱丄6g偵5偑擖傞壜擻惈偼偁傝傑偣傫丅,
丂丂佀6g偼3偵側傝傑偡丅偙傟埲崀偼拞媺偺媄朄偱夝愅偟夝摎傪摼傜傟傑偡丅
丂亂椺戣4亃丂丂丂丂丂丂丂丂丂丂丂丂亂搑拞宱夁亃丂丂丂丂丂丂丂丂丂丂亂悢婰擖亃丂丂丂丂丂丂丂丂丂丂丂亂XY僂僀儞僌亃丂丂丂丂丂丂丂丂丂亂夝摎亃

俁丏XYwing丂type2
丂type2偼忋媄朄侾偱3儅僗寛傔丄2僄儕傾偱懠偺儅僗偺悢帤傪寛掕偡傞曽朄偱偡丅巊梡昿搙偼type1傎偳懡偔偼偁傝傑偣傫偑丄type1偺摿庩宯偲傕偄偊傑偡丅
椺戣5偱偼拞塃偺F僄儕傾偲壓塃偺I僄儕傾偺2偮偺僄儕傾偺9f,9h,7i偲9f,9h,7d偺3偮偺儅僗偑丄24-27-47偺慻傒崌傢偣偵側偭偰偄傑偡丅偙偺椺戣偼丄XY僂僀儞僌偑2偮偁傞働乕僗偱偡丅3儅僗寛傔丄2僄儕傾偱懠偺儅僗偺悢帤傪寛掕偡傞偙偲偵側傝傑偡丅
嵍僒僀僪偺XY僂僀儞僌偱偼丄7d偑4偺応崌偵偼9f,9h偑嫟偵2偵側傝柕弬偲側傝傑偡偑丄7d偑7偺応崌偵偼柕弬偑惗偠傑偣傫偺偱丄7d偼7偵寛掕偟傑偡丅
塃僒僀僪偺XY僂僀儞僌偱偼丄7i偑7偺応崌偵偼9f,9h偑嫟偵2偵側傝柕弬偲側傝傑偡偑丄7i偑4偺応崌偵偼柕弬偑惗偠傑偣傫偺偱丄7i偼4偵寛掕偟傑偡丅
偙傟埲崀偼捠忢偺拞媺埲壓偺媄朄偱夝愅偱偒傑偡丅
丂
亂椺戣俆亃丂丂丂丂丂丂丂丂丂丂亂搑拞宱夁亃丂丂丂丂丂丂丂丂丂亂悢婰擖亃丂丂丂丂丂丂丂丂丂丂亂XY僂僀儞僌亃丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂夝摎亃

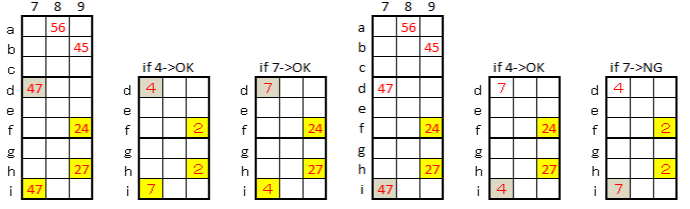
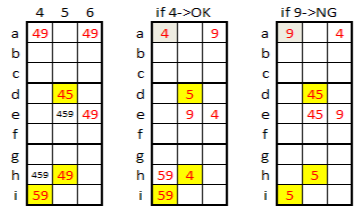
椺戣6偱偼拞拞偺E僄儕傾偲壓拞偺H僄儕傾偺2偮偺僄儕傾偺5d,5h,4i偑丄45-49-59偺慻傒崌傢偣偵側偭偰偄傑偡丅3儅僗寛傔丄2僄儕傾偱懠偺儅僗偺悢帤傪寛掕偡傞偙偲偵側傝傑偡丅4a偑4偺応崌偵偼柕弬偑惗偠傑偣傫偑丄4a偑9偺応崌偵偼5h,4i偑嫟偵5偵側傝柕弬偲側傝傑偡偺偱4a偼4偵寛掕偟傑偡丅
偙傟埲崀偼捠忢偺拞媺埲壓偺媄朄偱夝愅偱偒傑偡丅
丂亂椺戣俇亃丂丂丂丂丂丂丂丂丂丂丂丂亂搑拞宱夁亃丂丂丂丂丂丂丂丂丂亂悢婰擖亃丂丂丂丂丂丂丂丂丂丂丂亂XY僂僀儞僌亃丂丂丂丂丂丂丂丂丂丂亂夝摎亃

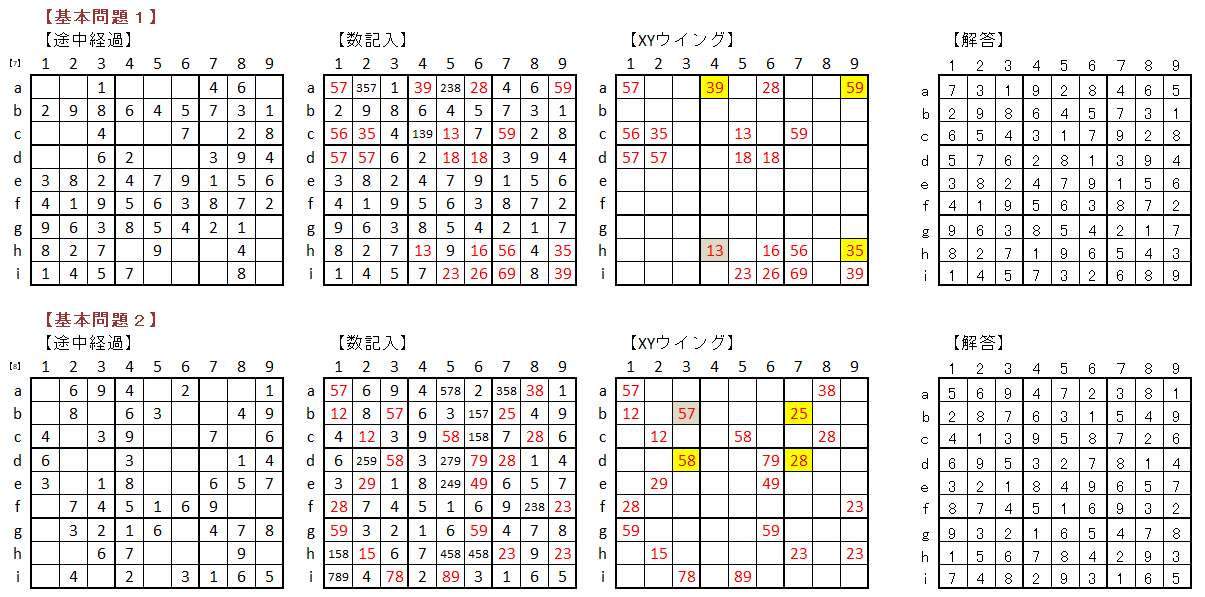
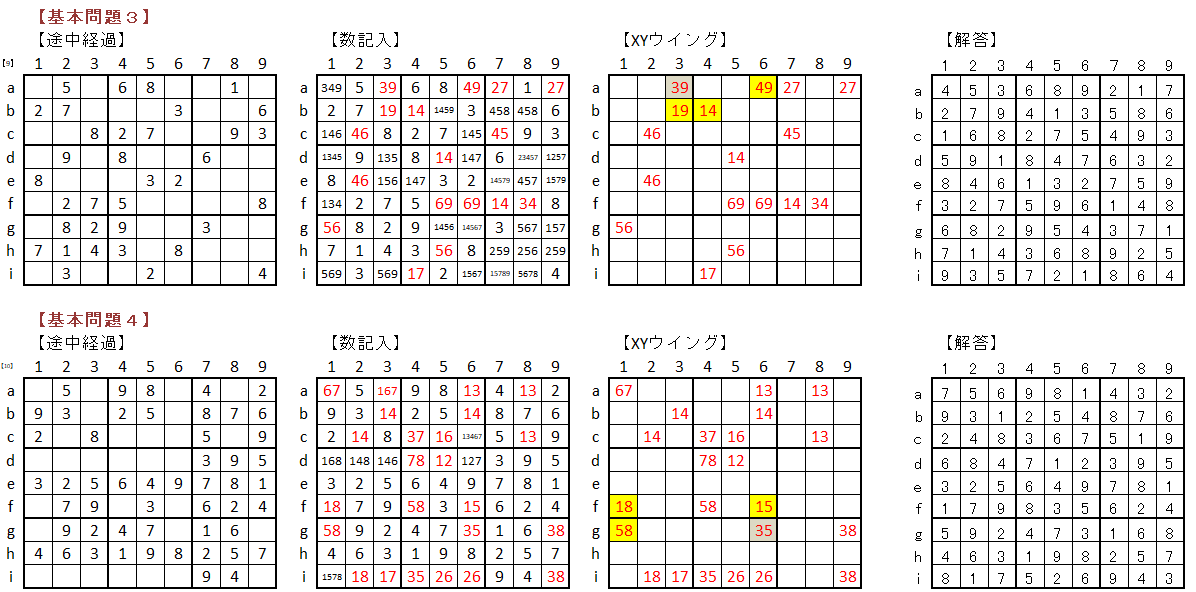
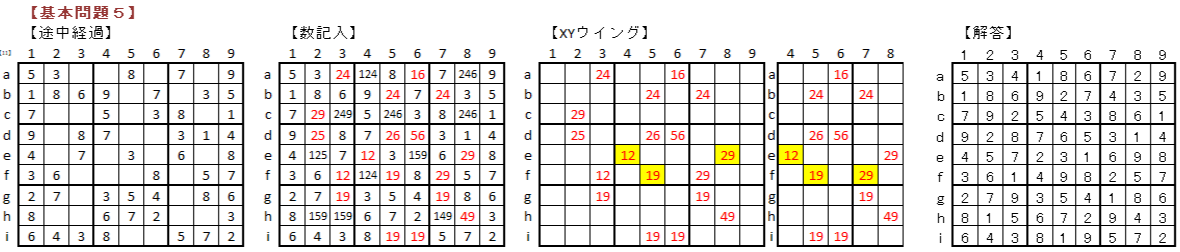
係丏婎杮栤戣
丂XY僂僀儞僌媄朄傪儅僗僞乕偡傞偨傔偵俆栤偺婎杮栤戣偵僠僃儗儞僕偟偰偔偩偝偄丅




仭丂婎杮栤戣夝摎丂仭